Logaritma

Rumus Logaritma

Nah, bagi anda yang belum kenal dengan logaritma, berikut kami jelaskan tentang pengertian logaritma dalam bahasa yang mudah dipahami. Pada dasarnya pengertian Logaritma adalah operasi matematika yang merupakan invers (kebalikan) dari eksponen atau pemangkatan. Contoh logaritma bentuk eksponen  bila dinyatakan dengan notasi logaritma adalah .

Dengan keterangan sebagai berikut :

• a = basis atau bilangan pokok
• b = hasil atau range logaritma
• c = numerus atau domain logaritma.

Catatan, penting untuk anda ketahui sebelum kita membahas lebih jauh tentang rumus logaritmabahwa penulisan  sama artinya dengan .

Sifat Logaritma

Berikut contoh sifat logaritma yang akan kami tuliskan dalam tabel logaritma dibawah ini.

Jika a>0, a ≠ 1, m ≠ 1, b>0 dan c>0, maka berlaku :

Intinya, rumus sifat yang perlu kita hafalkan adalah sebagai berikut. Beberapa rumus dasar atau sifat logartima yang perlu kita ketahui :

Rumus Persamaan Logaritma

Jika kita punya  maka 
Dengan syarat 
Pertidaksamaan logaritma
Jika kita punya  maka kita punya dua kondisi ,
Pertama, saat a>0 maka 
Kedua, saat 0<a<1 ( a diantara 0 dan 1 contohnya ½, ¼ , dst) maka .

Contoh Soal Logaritma Lengkap

1).        Jika log 2 = a

maka log 5 adalah …

jawab :

log 5 = log (10/2) = log 10 – log 2 = 1 – a (karena log 2 = a)

2).         √15 + √60 – √27 = …

Jawab :

√15 + √60 – √27

= √15 + √(4×15) – √(9×3)

= √15 + 2√15 – 3√3

= 3√15 – 3√3

= 3(√15 – √3)

3).       log 9 per log 27 =…

Jawab :

log 9 / log 27

= log 3² / log 3³

= (2. log 3) / (3 . log 3) <– ingat sifat log a^n = n. log a

= 2/3

4).       √5 -3 per √5 +3 = …

Jawab :

(√5 – 3)/(√5 + 3)

= (√5 – 3)/(√5 + 3) x (√5 – 3)/(√5 – 3) <– kali akar sekawan

= (√5 – 3)²/(5 – 9)

= -1/4 (5 – 6√5 + 9)

= -1/4 (14 – 6√5)

= -7/2 + 3/2√5

= (3√5 – 7)/2

5).     Jika a log 3 = -0,3 tunjukkan bahwa a = 1/81 3√9

Jawab :

ª log 3 = -0,3

log 3/log a = -0.3

log a = -(10/3)log 3

log a = log [3^(-10/3)]

a = 3^(-10/3) = 3^(-4) (3²)^(⅓ )

a= 1/81 3√9

6).       log (3a – √2) dengan basis 1/2. Tentukan nilai a!

Jawab :

[log (3a – √2)]/log(0.5) = -0.5

log (3a – √2) = -0.5 log 0.5 = log (1/√½)

3a – √2 = 1/√½

a = (2/3) √2

7) Jika   , maka  .

Penyelesaian :

Langkah pertama :

8.) Diketahui  dan 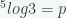. Nilai  dinyatakan dalam p dan q adalah … (UN SMA 2013)Penyelesaian :

9.)  Hasil dari  adalah …

Penyelesaian :

10.) 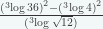    = …       (Sipenmaru 1987)

Penyelesaian :

Ingat sifat aljabar

Maka gunakan sifat tersebut untuk menyelesaikan pembilangnya.
Jadi,

Share: